current constant regardless of loading. The current being 'copied' can be, and sometimes is, a varying signal current. Conceptually, an ideal current mirror is simply an ideal
current amplifier. The current mirror is used to provide bias currents and active loads to circuits.
Mirror characteristics:
There are three main specifications that characterize a current mirror. The first is the current level it produces. The second is its AC output resistance, which determines
how much the output current varies with the voltage applied to the mirror. The third specification is the minimum voltage drop across the mirror necessary to make it work
properly. This minimum voltage is dictated by the need to keep the output transistor of the mirror in active mode. The range of voltages where the mirror works is called
the compliance range and the voltage marking the boundary between good and bad behavior is called the compliance voltage. There are also a number of secondary
performance issues with mirrors, for example, temperature stability.
Practical approximations:
For small-signal analysis the current mirror can be approximated by its equivalent Norton impedance .
In large-signal hand analysis, a current mirror usually is approximated simply by an ideal current source. However, an ideal current source is unrealistic in several
respects:
- it has infinite AC impedance, while a practical mirror has finite impedance
- it provides the same current regardless of voltage, that is, there are no compliance range requirements
- it has no frequency limitations, while a real mirror has limitations due to the parasitic capacitances of the transistors
- the ideal source has no sensitivity to real-world effects like noise, power-supply voltage variations and component tolerances.
Circuit realizations of current mirrors:
The simplest bipolar current mirror consists of two transistors connected as shown in Figure 1. Transistor Q1 is connected to ground. Its collector-base voltage is zero as
shown. Consequently, the voltage drop across Q1 is VBE, that is, this voltage is set by the diode law and Q1 is said to be diode connected. (See also Ebers-Moll model.) It is
important to have Q1 in the circuit instead of a simple diode, because Q1 sets VBE for the transistor Q2. If Q1 and Q2 are matched, that is, have substantially the same
device properties, and if the mirror output voltage is chosen so the collector-base voltage of Q2 also is zero, then the VBE-value set by Q1 results in an emitter current in
the matched Q2 that is the same as the emitter current in Q1. Because Q1 and Q2 are matched, their β0-values also agree, making the mirror output current the same as the
collector current of Q1. The current delivered by the mirror for arbitrary collector-base reverse bias VCB of the output transistor is given by (see bipolar transistor):
 ,
,where VT = thermal voltage, IS = reverse saturation current, or scale current; VA = Early voltage. This current is related to the reference current IREF when the output
transistor VCB = 0 V by:

when both transistors have zero base-collector bias, the two base currents are equal. Parameter β0 is the transistor β-value for VCB = 0 V.
Figure 1: A current mirror implemented with npn bipolar transistors using a resistor to set the reference current IREF; VCC = supply voltage
 ,
,
where VA = Early voltage and VCB = collector-to-base bias.
Compliance voltage:
Output resistance:
If VCB is greater than zero in output transistor Q2, the collector current in Q2 will be somewhat larger than for Q1 due to the Early effect. In other words, the mirror
has a finite output (or Norton) resistance given by the rO of the output transistor, namely (see Early effect):
If VCB is greater than zero in output transistor Q2, the collector current in Q2 will be somewhat larger than for Q1 due to the Early effect. In other words, the mirror
has a finite output (or Norton) resistance given by the rO of the output transistor, namely (see Early effect):
 ,
,where VA = Early voltage and VCB = collector-to-base bias.
Compliance voltage:
To keep the output transistor active, VCB ≥ 0 V. That means the lowest output voltage that results in correct mirror behavior, the compliance voltage, is VOUT = VCV = VBE
under bias conditions with the output transistor at the output current level IC and with VCB = 0 V or, inverting the I-V relation above:
where VT = thermal voltage and IS = reverse saturation current (scale current).
Extensions and complications:
When Q2 has VCB > 0 V, the transistors no longer are matched. In particular, their β-values differ due to the Early effect, with
where VA is the Early voltage and β0 = transistor β for VCB = 0 V. Besides the difference due to the Early effect, the transistor β-values will differ because the β0-values
depend on current, and the two transistors now carry different currents (see Gummel-Poon model).
Further, Q2 may get substantially hotter than Q1 due to the associated higher power dissipation. To maintain matching, the temperature of the transistors must be nearly
the same. In integrated circuits and transistor arrays where both transistors are on the same die, this is easy to achieve. But if the two transistors are widely separated,
the precision of the current mirror is compromised.
Additional matched transistors can be connected to the same base and will supply the same collector current. In other words, the right half of the circuit can be duplicated
several times with various resistor values replacing R2 on each. Note, however, that each additional right-half transistor "steals" a bit of collector current from Q1 due to
the non-zero base currents of the right-half transistors. This will result in a small reduction in the programmed current.
An example of a mirror with emitter degeneration to increase mirror resistance is found in two-port networks.
For the simple mirror shown in the diagram, typical values of β will yield a current match of 1% or better.
Obtenido de: http://en.wikipedia.org/wiki/Current_mirror

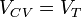



No hay comentarios:
Publicar un comentario