Figure is an example Widlar current source using bipolar transistors, where the emitter resistor R2 is connected to the output transistor Q2, and has the effect of reducing the current in Q2 relative to Q1. The key to this circuit is that the voltage drop across the resistor R2 subtracts from the base-emitter voltage of transistor Q2, thereby turning this transistor off compared to transistor Q1. This observation is expressed by equating the base voltage expressions found on either side of the circuit in Figure as:
Eq. 1
This equation makes the approximation that the currents are both much larger than the scale currents IS1, IS2, an approximation valid except for current levels near cut off. In the following the distinction between the two scale currents is dropped, although the difference can be important, for example, if the two transistors are chosen with different areas.
These considerations suggest the following design procedure:
- Select the desired output current, IO = IC2.
- Select the reference current, IR1, assumed to be larger than the output current, probably considerably larger. (That is the purpose of the circuit.)
- Determine the input collector current of Q1, IC1:
- Determine the base voltage VBE1 using the Shockley diode law
-
- Where IS is a device parameter sometimes called the scale current.
- The value of base voltage also sets the compliance voltage VA = VBE1. This voltage is the lowest voltage for which the mirror works properly.
- Determine R1:
The inverse of the design problem is finding the current when the resistor values are known. An iterative method is described next. Assume the current source is biased so the collector-base voltage of the output transistor Q2 is zero. The current through R1 is the input or reference current given as,
Eq. 2
Eq. 3
- We guess starting values for IC1 and IC2.
- We find a value for VBE1:
- We find a new value for IC1:
- We find a new value for IC2:
Note that with the circuit as shown, if VCC changes, the output current will change. Hence, to keep the output current constant despite fluctuations in VCC, the circuit should be driven by a constant current source rather than using the resistor R1.
Output Impedance
An important property of a current source is its small signal incremental output impedance, which should ideally be infinite. The Widlar circuit introduces local current feedback for transistor Q2. Any increase in the current in Q2 increases the voltage drop across R2, reducing the VBE for Q2, thereby countering the increase in current. This feedback means the output impedance of the circuit is increased, because the feedback involving R2 forces use of a larger voltage to drive a given current.
Output resistance is found using a small-signal model for the circuit, shown in Figure. The transistor Q1 is replaced by its small-signal emitter resistance rE because it is diode connected. The transistor Q2 is replaced with its hybrid-pi model. A test current Ix is attached at the output.

Using the figure, the output resistance is determined using Kirchhoff's laws. Using Kirchhoff's voltage law from the ground on the left to the ground connection of R2:
Eq. 4
Current Dependence of Output Resistance
The current dependence of the resistances rπ and rO is discussed in the article hybrid-pi model. The current dependence of the resistor values is:
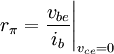
 in ohms, and
in ohms, and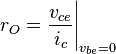
 is the output resistance due to the Early effect when VCB = 0 V (device parameter VA is the Early voltage).
is the output resistance due to the Early effect when VCB = 0 V (device parameter VA is the Early voltage).
Eq. 5
Eq. 6
Increase of IC1 to increase the feedback factor also results in increased compliance voltage, not a good thing as that means the current source operates over a more restricted voltage range. So, for example, with a goal for compliance voltage set, placing an upper limit upon IC1, and with a goal for output resistance to be met, the maximum value of output current IC2 is limited.
The center panel in Figure shows the design trade-off between emitter leg resistance and the output current: a lower output current requires a larger leg resistor, and hence a larger area for the design. An upper bound on area therefore sets a lower bound on the output current and an upper bound on the circuit output resistance.
Eq. 6 for RO depends upon selecting a value of R2 according to Eq. 5. That means Eq. 6 is not a circuit behavior formula, but a design value equation. Once R2 is selected for a particular design objective using Eq. 5, thereafter its value is fixed. If circuit operation causes currents, voltages or temperatures to deviate from the designed-for values; then to predict changes in RO caused by such deviations, Eq. 4 should be used, not Eq. 6.

Nombre: Rodriguez B. Joiver I.
Asignatura: EES




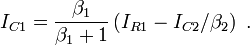

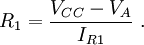

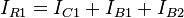
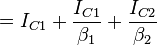
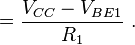










No hay comentarios:
Publicar un comentario